Guía de referencia para investigadores no expertos en el uso de estadística multivariada
Reference guide for non-expert researchers in multivariate statistics
Abstract (en)
New researchers often face difficulties in the statistical analysis of data for verification of the working hypotheses, particularly in the selection of an appropriate statistical technique, its application and interpretation. It is often argued that the foregoing of a negative attitude toward the quantitative analysis related to perceived difficulties in statistics classes and research methodology in education. The purpose of this article is to provide a reference guide for non-expert researchers in the use of some statistical techniques with broad applications in the generation of knowledge. Each multivariate technique is defined and the conditions under which it is possible its application are enumerated, presenting the minimum conditions to be met. In addition, three examples are presented showing inconsistencies resulting from a wrong use of statistics and assumptions in analyzing the data.
Abstract (es)
Quienes se inician en la investigación suelen encontrarse con dificultades en el análisis estadístico de los datos para la verificación de su hipótesis de trabajo, particularmente en la selección de la técnica estadística apropiada, su aplicación e interpretación. Se plantea que lo anterior resulta de una actitud negativa hacia el análisis cuantitativo, relacionado con dificultades percibidas en clases de estadística y metodología de la investigación en educación superior. El objetivo del presente artículo es ofrecer una guía de referencia para investigadores no expertos en el uso de algunas técnicas estadísticas con amplia aplicación en la generación de conocimiento. Se define cada técnica multivariada presentada y se especifican las condiciones en las cuales es posible su aplicación enumerando los supuestos mínimos que debe cumplir. Adicionalmente, se presentan tres ejemplos que muestran las inconsistencias estadísticas que resultan de no considerar algunos supuestos en el análisis de los datos.
References
Aparisi, F., Avendaño, G., & Sanz, J. (2006). Interpreting T2 Control Charts. IIE Transaccions, 38(8), 647-657.
Avendaño, G. (2003). Interpretación de la señal de falta de control en gráficos multivariantes mediante redes neuronales. (Doctorate Thesis), Universidad Politécnica de Valencia.
Bello, R., & Garcia, M. (1996). A model and its different applications to case-based reasoning. Knowledge System Design and Applications, 9(7), 465-473.
Berrendero, J. R., Justel, A., & Svarc, M. (2011). Principal components for multivariate functional data. Computacional Statistics and data analysis, 55(9), 2.619-2.634.
Conchillo, A. (2004). Guías doctorado. Metodología de las ciencias del comportamiento. España: Madrid: Universidad Nacional de Educación a Distancia (UNED).
Dallas, E. J. (2000). Métodos multivariados aplicados al análisis de datos. México: International Thomson Editores, S. A.
Daniel, W. (1998). Bioestadística. Base para el análisis de las ciencias de la salud. México: Noriega Editores.
Díaz, F., & Hernández, G. (2002). Estrategias docentes para un aprendizaje significativo. Una interpretación constructivista. México: McGraw-Hill.
Ferrán, M. (1996). SPSS para Windows. Programación y análisis estadístico. Madrid: McGraw-Hill.
Figueras, S. (2001). Análisis de conglomerados o clúster. Recuperado de http://www.5campus.org/leccion/cluster
Field, A. (2013). Discovering Statistics Using IBM SPSS Statistics. Fourth Edition. Londres: SAGE Publications Ltd.
Greene, J., & D'Oliveira, M. (2006). Test Estadísticos para Psicología. Madrid: McGraw-Hill.
Hair, J., Anderson, R., Tatham, R., & Black, W. (2000). Análisis Multivariante Quinta edición. Madrid: Prentice Hall.
Jackson, J. E. (1991). A user's guide to principal components. New York: John Wiley y Sons, Inc.
Jaques, J., & Preda, C. (2014). Model-based clustering for multivariate functional data. Computacional Statistics and data analysis. 71. 92-106.
Kerlinger, F., & Lee, H. (2002). Investigación del comportamiento. Métodos de investigación en ciencias sociales. México: McGraw-Hill.
Lizasoain, L., & Joaristi, L. (2003). Gestión y análisis de datos con SPSS. Versión 11. Madrid: Thompson.
López, C., Fernández, K., & Mariel, P. (2002). Índices de satisfacción del consumidor: una aplicación de modelos estructurales a la industria automovilística española. Universidad del país vasco.
Malhotra, N. (1997). Investigación de Mercados. Un enfoque práctico. México: Prentice-Hall.
Marques de Sá, J. (2007). Applied Statistics Using SPSS, STATISTICS, MATLAB and R. Second Edition. Heidelberg: Springer.
Martínez, C. (2000). Estadística y Muestreo. Bogotá: Ecoe editores.
Morales, P. (2003). El Análisis Factorial en la construcción e interpretación de tests, escalas y cuestionarios. Recuperado de http://www.upcomillas.es/personal/peter/investigacion/AnalisisFactorial.pdf
Murtonen, M. (2005). University Students' Research Orientations: Do negative attitudes exist toward quantitative methods? Scandinavian Journal of Educational Research, 49(3), 263-280.
Oquendo, D., de la Espriella, C., & Avendaño, B. L. (2007). Eventos de vida y alto afecto negativo como factores de riesgo para el desarrollo de depresión en jóvenes colombianos. (Magister), Fundación Universitaria Konrad Lorenz.
Romero, R. (1997). Curso de introducción a los métodos de análisis estadístico multivariante. Universidad Politécnica de Valencia.
Sánchez, F. (2006). Validación de una prueba para evaluar clima organizacional.
Visauta, B. (2002). Análisis Estadístico con SPSS para Windows. Segunda Edición. (Vol. 1). España: McGraw-Hill.
How to Cite
Guía de referencia para investigadores no expertos en el uso de estadística multivariada*
Reference guide for non-expert researchers in multivariate statistics
Bertha Lucía Avendaño Prieto**, Gerardo Avendaño Prieto***, William Cruz****, Alejandro Cárdenas-Avendaño*****
* Artículo de investigación.
** Facultad Psicología, Universidad Católica de Colombia, Bogotá, Colombia, Dirección postal: Av. Caracas No 46-72.
[email protected].
*** Universidad EAN, Colombia
**** National Chengchi University, Universidad de Taipei, República Popular de China
***** Fundación Universitaria Konrad Lorenz, Colombia
Recibido: 2 de junio de 2013 / Revisado: 30 de julio de 2013 / Aceptado: 10 de septiembre de 2013
Resumen
Quienes se inician en la investigación suelen encontrarse con dificultades en el análisis estadístico de los datos para la verificación de su hipótesis de trabajo, particularmente en la selección de la técnica estadística apropiada, su aplicación e interpretación. Se plantea que lo anterior resulta de una actitud negativa hacia el análisis cuantitativo, relacionado con dificultades percibidas en clases de estadística y metodología de la investigación en educación superior. El objetivo del presente artículo es ofrecer una guía de referencia para investigadores no expertos en el uso de algunas técnicas estadísticas con amplia aplicación en la generación de conocimiento. Se define cada técnica multivariada presentada y se especifican las condiciones en las cuales es posible su aplicación enumerando los supuestos mínimos que debe cumplir. Adicionalmente, se presentan tres ejemplos que muestran las inconsistencias estadísticas que resultan de no considerar algunos supuestos en el análisis de los datos.
Palabras clave: técnicas estadísticas, estadística multivariada, técnicas de dependencia, técnicas de interdependencia.
Abstract
New researchers often face difficulties in the statistical analysis of data for verification of the working hypotheses, particularly in the selection of an appropriate statistical technique, its application and interpretation. It is often argued that the foregoing of a negative attitude toward the quantitative analysis related to perceived difficulties in statistics classes and research methodology in education. The purpose of this article is to provide a reference guide for non-expert researchers in the use of some statistical techniques with broad applications in the generation of knowledge. Each multivariate technique is defined and the conditions under which it is possible its application are enumerated, presenting the minimum conditions to be met. In addition, three examples are presented showing inconsistencies resulting from a wrong use of statistics and assumptions in analyzing the data.
Keywords: Statistical techniques, multivariate statistic, dependence interdependence techniques.
La enseñanza es una práctica cotidiana que tiene lugar a lo largo de nuestras vidas y se enmarca en la interacción humana, cualquier situación en la cual se tenga por objetivo la creación y transferencia de conocimiento, requiere tanto de la destreza de quien aprende para integrar nueva información y habilidades mediante su interés, su memorización y su práctica, como de la destreza de quien enseña para organizar dicha información, hacerla llamativa y asimilable a otros.
El modelo tradicional de la educación concibe el aprendizaje en una única dirección, siendo el profesor el punto de origen y el estudiante el punto de llegada, omitiendo la posibilidad de una reelaboración activa del conocimiento que está siendo transmitido y de un aprendizaje mutuo en dicha interacción. Díaz & Hernández (2002) señalan que la práctica pedagógica es eficaz cuando se tiene en cuenta el conocimiento de partida del alumno y se cuestiona alrededor de este.
Murtonen (2005) sugiere que los estudiantes universitarios de primer año inician sus clases con actitudes, creencias y expectativas acerca de la educación y su propósito, las cuales han elaborado a partir de su propia experiencia basadas en ideas en torno a la construcción del conocimiento; es decir, una posición epistemológica. Asimismo señala que dichas ideas guían los estándares de comprensión y las estrategias de estudio empleadas por cada estudiante, de modo tal que la actitud de partida hacia las matemáticas o la estadística, por ejemplo, modula las experiencias de aprendizaje subsiguientes facilitando o dificultando su aprendizaje, comprensión, uso y transmisión.
Los estudiantes interesados en la investigación suelen percibir dificultades en el análisis estadístico de los datos, particularmente en la selección de la prueba estadística apropiada, su aplicación e interpretación.
Dicha percepción es un correlato de una actitud negativa hacia los métodos cuantitativos, resultado de diversos factores tales como la atribución irreal de dificultad hacia los procedimientos estadísticos y la antigua creencia sobre su poco uso en la vida laboral (Murtonen, 2005).
Los aspectos mencionados dificultan las iniciativas de investigación y se percibe la necesidad de un documento que oriente la comprensión de los conceptos utilizados en estadística multivariada. Este artículo a modo de guía intenta complementar los contenidos que se imparten en las clases de estadística y metodología de la investigación a nivel de pregrado y posgrado, con el objetivo de acercar a los estudiantes a los procesos de creación del conocimiento.
Tras la recolección, organización y filtración de las observaciones disponibles en una base de datos, surge la necesidad de aplicar uno o varios procedimientos estadísticos para su análisis, lo cual demanda una comprensión acerca de los supuestos y el alcance de la utilización de una prueba estadística frente a otra o de su combinación. De tal modo es indispensable que el investigador esté familiarizado con las técnicas de análisis estadístico, dada la multiplicidad de contextos de aplicación, versatilidad para lidiar con la creciente cantidad de información disponible en bases de datos, desarrollo del software estadístico y necesidad e interés humano de continuar generando conocimiento en torno al mundo que le rodea.
En primer lugar un análisis estadístico exige la identificación del nivel de medición de las variables; esto es, definir la tipología de cada variable al interior de las siguientes opciones: a) nominal, b) ordinal, c) de intervalo o d) de razón, de lo cual dependerá la selección de estadísticas descriptivas en el análisis preliminar (i.e. se elaboran tablas de frecuencias y porcentajes para las variables del tipo a y b; y se calculan los estadísticos de tendencia normal, box plot e histogramas para las variables del tipo c o d).
Posteriormente se identifican y enumeran el tipo de relaciones posibles (y de interés) entre las variables disponibles (i.e. si es plausible una relación de dependencia o interdependencia entre un par o grupo de variables), lo cual está vinculado a los objetivos iniciales de investigación y a la idoneidad de dichas mediciones para evaluar la hipótesis de trabajo. Seguidamente y teniendo en cuenta lo anterior, se seleccionan las técnicas estadísticas a utilizar con base en sus supuestos, ventajas y limitaciones. En caso de no seguir este esquema de trabajo, no es posible garantizar que el análisis de los datos sea correcto ni la validez de los hallazgos. Finalmente, y no menos importante, el investigador debe escoger una forma adecuada de visualizar los resultados para su difusión, buscando atraer también a un lector no especializado.
Análisis multivariado
El análisis multivariado,
agrupa un conjunto de técnicas estadísticas cuyo objetivo principal es estudiar la interacción y/o correlación entre variables, para generar inferencias y predicciones; en otras palabras, constituye una familia de métodos de análisis que estudia de manera simultánea varias variables independientes y una o más variables dependientes (Kerlinger, 2002).
Es importante aclarar lo siguiente:
Los conceptos de individuo, grupo y variable pueden corresponder a realidades muy distintas de acuerdo al problema considerado, por lo tanto un conocimiento teórico amplio sobre el tema de investigación proporciona pistas acerca de los fundamentos epistemológicos para dar cuenta de dicho fenómeno (Romero, 1997).
Los contextos de aplicación de los métodos a presentar son variados y numerosos, siendo su finalidad amplia para la descripción de las relaciones entre dos o más variables para generar predicciones, la obtención de una visión comprehensiva sobre la estructura interna de los datos y el establecimiento de grupos con base en diferentes criterios. Otras aplicaciones más específicas incluyen el establecimiento de niveles de fidelidad por parte de los clientes con base en sus percepciones, la identificación de segmentos de mercado con base en la preferencia hacia productos y servicios, la estimación sobre la competitividad o similitud de distintos productos con base en los patrones de consumo, la realización de controles estadísticos sobre procesos de producción, la elaboración de modelos que permitan analizar procesos psicológicos, neuropsicológicos, psicosociales, clínicos, jurídicos, organizacionales, educativos y comunitarios, entre otros. En suma, estas técnicas estadísticas asisten en la generación de modelos predictivos, con la finalidad de clasificar, reconocer y explicar patrones o anomalías (Hair, Anderson, Tatham, & Black, 2000).
Es posible distinguir el análisis multivariado en dos categorías; de Dependencia o Interdependencia entre las variables. Las técnicas de Dependencia involucran un grupo de Variables Independientes (Vl's) para predecir y explicar el cambio en una o más Variables Dependientes (VD's). En contraste, las técnicas de Interdependencia no definen a priori ninguna variable como independiente o dependiente; es decir, el procedimiento implica el análisis de todas las variables conjunta y simultáneamente (Hair et al., 2000).
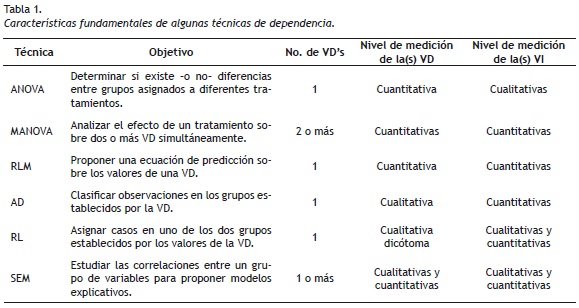
La prueba básica de todos los procedimientos multivariados es el Análisis de Varianza o ANOVA de un factor; esta técnica es una extensión de la comparación de medias para dos muestras que realiza la prueba t de Student. El ANOVA, por sus siglas en ingles Analysis Of Variance (Greene & D'Oliveira, 2006), es aplicable en situaciones con dos o más grupos cuya clasificación está determinada por la VI (Visauta, 2002). Se utiliza para indagar sobre el efecto de una VI con dos o más condiciones sobre una VD (e.g. el efecto del tipo de Afasia, sobre el desempeño en un test de fluencia verbal). Su objetivo principal es analizar si hay -o no- diferencias estadísticamente significativas entre las medias de los grupos considerados evaluando su varianza; lo cual se realiza a partir de la comparación de la varianza entre grupos junto con la varianza al interior de cada grupo (i.e. usualmente referenciada en los textos y programas estadísticos como between y within comparison respectivamente).
De tal modo el ANOVA de un factor constituye el fundamento estadístico de otros métodos, tales como el Análisis Factorial (AF), el Análisis Multivariado de Varianza (MANOVA), los modelos con factores de efectos fijos, aleatorios, de medidas repetidas, el diseño de bloques completos aleatorizados, entre otros (Daniel, 1998; Ferrán, 1996).
Técnicas de Dependencia
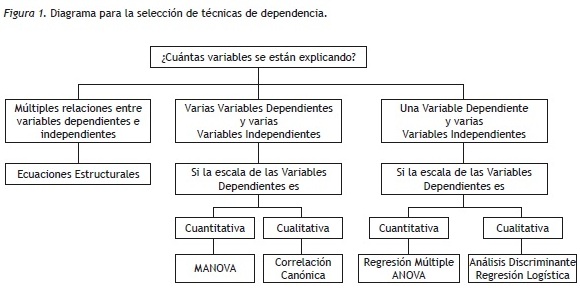
A continuación se presenta un diagrama de flujo con técnicas de Dependencia basado en un figura de Hair et al. (2000), la cual indica la relación entre las VD y las VI junto con el nivel de medición que exige cada técnica (Figura 1).
De las técnicas de dependencia mencionadas en la Figura 1, se expondrán el MANOVA, la Regresión Lineal Múltiple (RLM), el Análisis Discriminante (AD), la Regresión Logística (RL) y los Modelos de Ecuaciones Estructurales (SEM), herramientas para el análisis estadístico con amplia aplicación en la investigación.
Análisis Multivariado de Varianza (MANOVA)
Esta técnica es una extensión del ANOVA, pero a diferencia de esta, considera dos o más VD simultáneamente. El MANOVA es una técnica de Dependencia que permite estimar las diferencias entre las medias de varias categorías o tratamientos, mediante la comparación conjunta de las VD observadas. Las categorías vienen dadas por el conjunto de criterios que definen distintos estados, cuadros patológicos, grupos humanos, dosis, tratamientos, etc. Las condiciones necesarias para utilizar el MANOVA son: a) hay varios tratamientos que se definen por el grado, la ausencia o presencia de una VI, b) al interior de cada tratamiento hay varios individuos o sujetos, y c) las mediciones para cada individuo o sujeto son independientes.
En suma, se realiza un MANOVA cuando el investigador diseña una situación experimental con varios tratamientos, para evaluar hipótesis concernientes a la varianza de los desempeños grupales en dos o más VD cuantitativas (Dallas, 2000; Hair et al., 2000).
Un ejemplo del uso del MANOVA puede encontrarse en Malhotra (1997), quien presentó cuatro comerciales de una marca de jabón X a cuatro grupos de consumidores, de modo tal que cada grupo de consumidores veía una variación posible del comercial; tras verlo, las personas en cada grupo otorgaron calificaciones sobre la preferencia por el jabón y la compañía comercializadora entre otras características. Dado que se espera que las tres VD se correlacionen entre sí, es apropiado realizar un MANOVA para determinar el comercial hacia el cual se obtienen puntuaciones más favorables, para asistir en la elección del comercial que será parte de la campaña publicitaria. A continuación se enumeran los supuestos estadísticos de esta técnica.
Supuestos
Las variables se distribuyen de manera normal por separado, lo cual se evalúa mediante las pruebas de Kolmogorov-Smirnov, Shapiro-Wilk o el gráfico Q-Q normal1.
Las variables se distribuyen de manera normal en conjunto, lo cual se evalúa mediante los test de Mardia2.
Las varianzas de cada variable resultan iguales cuando son comparadas entre los grupos (homocedasticidad), lo cual se evalúa mediante el test de Box3 y su valor F asociado).
Los coeficientes de correlación (usualmente r de Pearson) entre dos variables para un mismo grupo son comparables, asimismo para todos los grupos.
Las variables dependientes se correlacionan entre sí (Dallas, 2000; Ferrán, 1996; Hair et al., 2000).
Regresión Lineal Múltiple
Es una técnica estadística de dependencia utilizada para analizar la relación entre una o más VI (con poder predictivo) y una VD o de criterio. La RLM utiliza las VI, cuyos valores son conocidos, para predecir el valor de la VD. Cada variable es ponderada, de forma que su ponderación o la estimación de su contribución relativa, resulta en la determinación de coeficientes de regresión en una función lineal (Hair, et al, 2000).
Con este método se estudia la forma en que las puntuaciones de la VD o Y "regresan hacia" o "dependen de", las puntuaciones de las VI (x1 x2 xn) (Kerlinger & Lee, 2002). La regresión de Y con base en las VI se expresa por medio del coeficiente de determinación R2, el cual representa la proporción de la varianza de la VD, explicada por las VI.
El modelo matemático o la expresión de la función en la RLM es idéntica a la utilizada por el ANOVA (Ecuación 1). Los parámetros b se denominan coeficientes de regresión. El coeficiente bf por ejemplo, representa el aumento o disminución de la VD, cuando la primera VI o x1 aumenta en una unidad, si se mantienen constantes las otras variables. Siempre que las VI en la ecuación permanezcan constantes, los coeficientes de regresión determinarán un punto respecto a la ordenada y se interpretarán de la misma manera (Martínez, 2000).
El modelo ofrece una ecuación de regresión con las características de una fórmula de predicción para futuras observaciones. Una gran parte de investigadores en las ciencias sociales utilizan la RLM para estimar los valores de la VD con propósitos de selección, pero sus aplicaciones no se reducen a dicha situación (Kerlinger & Lee, 2002).
Los coeficientes de regresión no son totalmente estables y varían en relación con la muestra y la adición o sustracción de VI en el análisis, entre otras varias condiciones; de tal manera que su interpretación debe contemplar dicha limitación. Adicionalmente la magnitud de estos coeficientes es relativa, dado que un coeficiente determinado para dos variables en distintas unidades de medida, puede indicar una importancia relativa diferente. Para eliminar el efecto de las distintas unidades de medida sobre las VI, se recomienda considerar los coeficientes de regresión tipificados (Ferrán, 1996). Por otro lado, la situación ideal para predecir con un pequeño margen de error, tiene lugar cuando las correlaciones entre las VI y la VD son altas, y las correlaciones entre las VI son bajas (Kerlinger, 2002).
Supuestos
La VD y las VI son cuantitativas.
Las varianzas entre las variables son iguales (homocedasticidad).
La relación entre la VD y las VI corresponde a un modelo lineal, lo cual se corrobora si la distribución es normal.
Las variables independientes no están correlacionadas, no existe colinealidad.
Los errores son independientes (i.e. la puntuación de un individuo no debe estar relacionada con las obtenidas por los demás) (Lizasoain & Joaristi, 2003).
Análisis Discriminante
El Análisis Discriminante (AD) es ampliamente conocido como una técnica de clasificación (Dallas, 2000); es un método de Dependencia que clasifica objetos, personas u observaciones con base en la medición de varios atributos de dichos casos.
El AD permite identificar el grupo al cual pertenece un caso; se utiliza cuando la muestra puede dividirse en grupos con base en una VD que proporciona categorías identificables y excluyentes. El objetivo principal de esta técnica es entender las diferencias entre los grupos, permitiendo predecir la probabilidad de que un caso pertenezca a un grupo en particular, a partir de varias VI cuantitativas. Por ejemplo, puede utilizarse para distinguir consumidores y no-consumidores de un producto, de acuerdo con las puntuaciones en sus perfiles demográficos y psicográficos. Otras aplicaciones incluyen la distinción entre usuarios habituales, ocasionales y no usuarios de un servicio; también es utilizado en medicina o en psicología, para determinar la predisposición a una enfermedad, teniendo en cuenta los resultados de los exámenes médicos y o test psicológicos.
Cuando el análisis incluye dos clasificaciones, la técnica es conocida como AD de dos grupos; cuando se incluyen tres o más, la técnica es conocida como AD múltiple (Hair et al., 2000).
Otro aspecto del AD es que tiene una finalidad doble; un fin descriptivo, que consiste en evidenciar las diferencias grupales respecto al conjunto de variables utilizado para dividir una población; y un fin predictivo, que consiste en aportar procedimientos sistemáticos de clasificación para nuevas observaciones (Figueras, 2001).
Supuestos
La VD es cualitativa, con dos o más categorías.
Las VI son cuantitativas.
Las varianzas de las variables analizadas en los diversos grupos son iguales (homocedasticidad).
Las VI se distribuyen en forma normal con varianzas y covarianzas iguales (lo cual se estima mediante el método de Wilks' Lambda4 y el test de Box).
Regresión Logística
Con esta técnica se estudia la relación de una o más variables independientes con una variable dependiente cualitativa dicótoma (Visauta, 2002). Una variable dicótoma solo admite dos categorías que definen opciones o características mutuamente excluyentes u opuestas, tales como si-no, 0-1, acierto-error, fuma-no fuma, vivo-muerto, entre otras categorías posibles.
Un modelo de RL permite estimar o predecir la probabilidad de que un individuo posea una de las condiciones (e.g. buen o mal rendimiento académico), en función de unas determinadas características individuales (e.g. xf = edad, x2 = estrato, x3 = actitud hacia el estudio, xn), tal como en el caso de la RLM. La diferencia fundamental entre la RLM y la RL, es que la primera técnica predice el valor medio de la VD o Y a partir de una o más VI (e.g. x1, x2, xn); mientras que la segunda, permite predecir la probabilidad de ocurrencia de una de las dos categorías de la VD, en función de una o más VI.
Supuestos
La VD es cualitativa y dicótoma.
Las VI no están correlacionadas (e.g. no existe colinealidad).
El número mínimo de casos para realizar estimaciones con un modelo de k VI es de 10 (k + 1). Es decir, por cada variable que interviene en el modelo, incluyendo la variable dependiente, se necesitan al menos 10 casos.
Modelos de Ecuaciones Estructurales (SEM)
Esta técnica relaciona VD y VI, permitiendo incorporar constructos no medidos en estas relaciones; de tal manera que, una VD puede ser al mismo tiempo, para otro conjunto de variables, una VI (Hair, et al, 2000). Desde los SEM se considera que toda teoría implica un conjunto de correlaciones; si la teoría es correcta debe ser posible reproducir los patrones de correlación (i.e. los supuestos) en datos empíricos.
Los SEM constituyen una de las herramientas más potentes para el estudio de relaciones causales sobre datos no experimentales cuando estas relaciones son de tipo lineal o unidireccional. Sin embargo, estos modelos no implican causalidad, únicamente filtran las hipótesis causales relevantes, eliminando aquellas que no son apoyadas por la evidencia empírica (López, Fernández, & Mariel, 2002).
Los SEM son una combinación del AF con la RLM, es una técnica confirmatoria y requiere que el investigador, con base en la teoría, defina la dirección de las correlaciones plausibles entre las variables. Incluye un conjunto de procedimientos que evalúan modelos de relaciones causales postulados desde la teoría sobre la relación entre variables observadas y variables latentes.
Supuestos
Los datos se distribuyen normalmente. Si la distribución no es normal, se deben aplicar transformaciones o la exclusión de casos extremos.
No existe colinealidad entre las VI, en caso contrario, los coeficientes deben ser menores a 80.
Un número mínimo de observaciones de 200 casos.
La relación entre las variables es lineal.
Las VI son de razón o de intervalo, en tanto que las VD pueden ser nominales.
Técnicas de Interdependencia
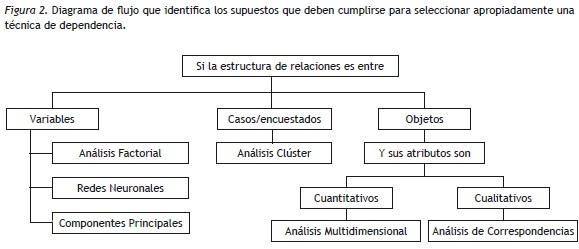
A continuación se presenta un diagrama con algunas técnicas de Interdependencia (Figura 2). De las técnicas presentadas se expondrán el Análisis Factorial (AF), las Redes Neuronales (RN), el Análisis de Componentes Principales (ACP) y el Análisis Clúster (AC).
Análisis Factorial (AF)
Es una técnica que permite crear nuevas variables, las cuales resumen la estructura de los datos y facilitan la interpretación de la estructura interna de los datos. El AF examina los patrones y relaciones subyacentes entre las variables iniciales, lo cual resulta en un número menor de variables denominados factores. Principalmente hay dos tipos de AF, a) el AF Exploratorio (AFE) y b) el AF Confirmatorio (AFC). En el AFE se busca obtener la mejor estructura de las interrelaciones entre las variables (i.e. enfocado en la reducción de datos), mientras que en el AFE el investigador genera una hipótesis previa sobre el número de factores y las variables que constituyen cada uno de estos y busca confirmar si los datos se ajustan -o no- a la estructura impuesta.
La varianza total de cada variable se divide en tres: comunalidad, que hace referencia a la varianza compartida entre las variables de la matriz de datos; específica, se refiere a la varianza que no es compartida con otras variables; y residual, la cual se debe a los errores de medición.
La comunalidad de una variable representa la proporción de varianza que está explicada por todos los factores y es común a estos. Se utiliza como criterio para decidir cuáles variables se mantendrán en el análisis; de tal modo que si una variable presenta baja comunalidad contribuye poco a la solución factorial y es preferible excluirla (Conchillo, 2004).
La saturación es el peso relativo de la variable en el factor, e indica la contribución de la variable a dicho factor, mientras que el cuadrado de la saturación representa la proporción de varianza compartida entre el factor y la variable. Por otro lado, el valor propio de un factor o el autovalor, representa la parte de varianza explicada por el factor y la suma de todos los autovalores, establece la varianza total de la muestra.
La interpretación de un factor se genera en relación con las variables que lo conforman y con los principios que guiaron la selección inicial de las variables. Para que la interpretación sea correcta las variables han de considerarse relevantes para el problema en cuestión y es en función de relaciones inicialmente propuestas, que el investigador recolecta datos y hace mediciones en un AF del tipo Exploratorio (Conchillo, 2004). En suma el AF presenta la agrupación de los ítems o variables con la menor pérdida de información y asiste en la conceptualización de los factores o variables latentes (Morales, 2003). Los supuestos básicos del AF son más de tipo conceptual que estadístico, exigiendo un conocimiento teórico amplio por parte del investigador al momento de explicar la estructura resultante.
Supuestos
El establecimiento del tamaño muestral depende de a) la proporción de sujetos respecto al número de variables y b) del número mínimo recomendable de sujetos en términos absolutos. Un criterio plausible es utilizar una muestra 10 veces mayor que el número de variables (N = 10k) (Conchillo, 2004; Morales, 2003). Otro criterio es N ≥ 200 y un mínimo de 5 observaciones por variable.
Conocimiento sobre el tema tratado, puesto que las conclusiones se fundamentan en este y la técnica no ofrece medios para determinar la conveniencia de las variables seleccionadas (Hair et al., 2000).
Normalidad de las variables (lo cual se evalúa mediante el test de esfericidad de Bartlett)5.
Correlaciones entre las variables (lo cual se establece mediante el índice Kaiser-Meyer-Olkin o KMO)6.
Análisis Clúster
Es un conjunto de técnicas utilizadas para clasificar los objetos o casos, en grupos relativamente homogéneos que se denominan conglomerados o clústers. Se espera que los objetos en cada grupo (clúster) sean similares entre sí (i.e. alta homogeneidad al interior del clúster) y diferentes a los objetos de otros grupos (i.e. alta heterogeneidad entre clústers), respecto a algún criterio de selección predeterminado. Al no distinguir entre VD y VI, se constituye en una técnica exploratoria diseñada para revelar agrupaciones naturales dentro de una colección de datos, calculando las relaciones interdependientes del conjunto de variables. Este análisis también es conocido como análisis de clasificación, taxonomía numérica y reconocimiento de patrones (Figueras, 2001).
Usualmente no se emplea ningún modelo estadístico que determine el proceso de clasificación, siendo ideal para extraer información de un conjunto de datos y útil en la elaboración de hipótesis acerca del problema considerado, sin imponer patrones o teorías previamente establecidas. Sin embargo y al igual que el AF, el conocimiento del investigador sobre el problema es fundamental al momento de decidir cuáles de los grupos obtenidos son significativos -y cuáles no-, de otro modo la clasificación de los datos puede resultar en una partición aleatoria de los mismos.
El AC es una técnica exploratoria y no se recomienda su uso para formular teorías, sus soluciones dependen de varios elementos del procedimiento y se obtienen diversas soluciones variando solo algunos casos; por otro lado la solución dependerá de la medida de comparación seleccionada. Aunque los resultados del AC pueden tomarse como punto de partida en la elaboración de teorías, no es una técnica inferencial dado que no es posible generalizar los hallazgos de la muestra a la población (Conchillo, 2004).
Supuestos
Conocer el tema tratado.
Las variables son cuantitativas.
Análisis de Componentes Principales
El Análisis de Componentes Principales (ACP) se utiliza para analizar las interrelaciones de un gran número de variables y explicarlas en términos de sus dimensiones comunes, reduciendo la información contenida en el número de variables originales, a un conjunto menor de variables con poca pérdida de información (Hair et al., 2000).
También se denomina método de proyección pues refleja en pocos componentes la información conjunta de las variables extrayendo la información de todos los datos simultáneamente, maneja bien el problema de datos faltantes y su gráfica es de fácil interpretación; es una técnica exploratoria que permite generar hipótesis en lugar de probarlas (Jackson, 1991).
Cuando las variables estudiadas se correlacionan entre sí, se utiliza el ACP para reducir el número de las mismas y encontrar componentes que expliquen la variación entre los factores, con óptimas propiedades y sin perder su generalidad.
Aunque el paquete estadístico para las ciencias sociales SPSS presenta el AF basado en el método de componentes principales, Dallas (2000) hace una distinción entre ambos análisis; en el AF se utiliza la varianza común o comunalidad entre la variables, mientras que en el ACP se utilizan todas las varianzas de la variable; esto es, la comunal, la específica y la residual. Aunque los primeros factores tienen varianza específica y residual, en el PCA suele suceder que los últimos factores se corresponden con una única variable. Los resultados de la investigación empírica no muestran grandes diferencias entre ambos procedimientos, aunque se ha generalizado el uso del ACP debido a la indeterminación de los factores en el AF (Conchillo, 2004).
El propósito del ACP es detectar relaciones poco evidentes a partir de la varianza de los datos, asumiendo que los componentes principales representan significativamente la totalidad de casos encontrados en los datos; si es así, el ACP puede usarse eficientemente.
Supuestos
Las unidades de medición de las variables utilizadas son equiparables.
Existe linealidad entre las variables.
La varianza de las variables consideradas es amplia.
Los componentes principales son ortogonales.
Redes Neuronales
Son modelos computacionales que pretenden simular la actividad cerebral mediante el desarrollo de una arquitectura con los rasgos funcionales de este órgano (Bello & García, 1996). Se define al cerebro como un equipo integrado por aproximadamente 10 billones de unidades de procesamiento (i.e. neuronas) que trabajan paralelamente con velocidad de cálculo lenta, pero debido a dicho paralelismo alcanzan alta potencia (Avendaño, 2003).
A partir de esta visión del cerebro se han elaborado paquetes informáticos como el QNET y MATLAB que trabajan con un conjunto de elementos computacionales simples (v.g unidades o celdas), los cuales constituyen neuronas artificiales vinculadas por arcos dirigidos que permiten su comunicación.
Las redes neuronales tienen diversas propiedades que las identifican:
Facilidad de funcionamiento: se utilizan potentes algoritmos para determinar el peso de las variables que conducen a una solución adecuada, a partir de ejemplos de entrenamiento (i.e. aprendizaje heurístico). Este procedimiento evita la utilización de lenguajes de programación.
Facilidad de representación: se ofrecen formas apropiadas de representar el conocimiento para ciertas clases de problemas, especialmente los de reconocimiento o clasificación.
Paralelismo: trabajo simultáneo de una gran cantidad de unidades de procesamiento (v.g. se puede calcular el nivel de actividad de todas las neuronas en un momento determinado).
Tolerancia al error: al haber varias unidades de procesamiento, cada una responsable de una parte pequeña de la tarea, y si algunas de estas unidades falla, el efecto en el resultado total del sistema no sería apreciable.
Dualidad en el trabajo: en el procesamiento pueden distinguirse dos fases, la fase de aprendizaje durante la cual los datos (i.e. pares de vectores con sus entradas y salidas correspondientes) se toman como el conjunto de entrenamiento para programar la red; es decir, para ajustar los pesos y las salidas asociadas (Aparisi, Avendaño, & Sanz, 2006).
Supuestos
Las variables son cualitativas y cuantitativas.
Se deben realizar varios ensayos para la obtención de la solución más adecuada.
Algunos usos incorrectos del análisis multivariado
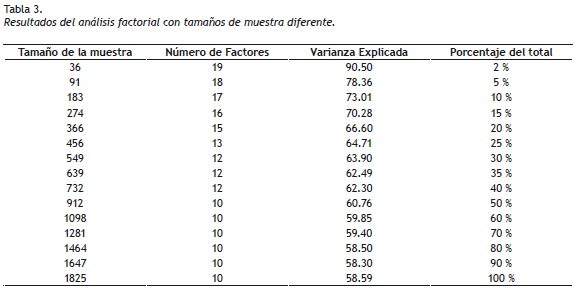
A continuación se ejemplifican algunos errores que se derivan de no considerar los supuestos de las técnicas anteriormente presentadas. En primer lugar se utilizan los resultados de un AF con datos reales, obtenidos de la aplicación de una prueba diseñada para medir clima organizacional (Sánchez, 2006). La prueba consta de 79 ítems que se aplicaron en 3 países a una muestra de 1.825 empleados de 14 áreas de trabajo, pertenecientes a 5 niveles jerárquicos de una empresa multinacional. El sustento teórico de la prueba suponía la existencia de 9 factores que integraban el clima organizacional, sin embargo al efectuar el análisis factorial, se encontraron 10 factores que explicaban el 58.59% de la varianza; resultado aproximado a lo teóricamente esperado. La Tabla 3, presenta los resultados encontrados al realizar el análisis con diferentes tamaños de muestra.
De acuerdo con los supuestos del AF y teniendo en cuenta el número de ítems de la prueba (k = 79), el número mínimo de personas recomendado para su aplicación es n = 790. En la Tabla 3 puede observarse que con tamaños de muestra inferiores a dicho valor, los resultados sobrevaloran los alcances de la prueba y se concluye que más del 62% de la varianza se explica con tamaños de muestra más pequeños. Para una muestra de 36 personas por ejemplo, la prueba arroja 19 factores que explican el 90.5% de la varianza. Es de resaltar el error en el cual se incurre cuando se encuentran 8 factores adicionales y 29.74% de diferencia en la varianza explicada, respecto a lo que se puede inferir de la prueba cuando se cumple este supuesto.
Con previa autorización de los autores y para efectos del siguiente ejemplo, (Oquendo, de la Espriella, & Avendaño, 2007), se utilizan los datos de un estudio en el que participaron 5.493 jóvenes con edades entre los 10 y 18 años, que tenía como objetivo identificar la relación entre factores de riesgo-alto de afecto negativo y el desarrollo de depresión. La variable dependiente fue la depresión y se utilizó la prueba Zung para su medición, las variables independientes fueron los factores de riesgo y el alto afecto negativo, medidos con las pruebas Eventos Vitales y Panas, respectivamente.
Al verificar todos los supuestos que exige la RLM, se encontró que las VI se correlacionaban entre sí; por tal motivo, las autoras realizaron dos regresiones lineales simples que permitieron identificar la correlación entre cada VI con la VD. La correlación entre el afecto negativo y la depresión fue de 0.79 (p = 0.001), en tanto que la correlación entre los eventos vitales y la depresión fue de 0.23 (p = 0.48); la segunda correlación no fue significativa, aspecto determinante para no utilizar la RLM; en caso de omitirse este supuesto, se encontraría que la varianza de la VD (v.g. la depresión), se explica en un 64% por ambas VI (v.g. factores de riesgo-afecto negativo), resultado que oculta cuál de las variables predice con mayor confianza la depresión.
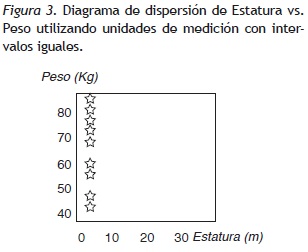
Por último se presenta un ejemplo que utiliza el ACP para el cual se ajustaron los datos al supuesto de unidades iguales en cada variable. Si por ejemplo se correlaciona el peso con la estatura, utilizando escalas de intervalos iguales se encontraría algo similar a lo expuesto en la Figura 3, la cual muestra una variable principal (i.e. el peso) y la variable secundaria que tiene el mismo valor para todos los individuos (i.e. la estatura).
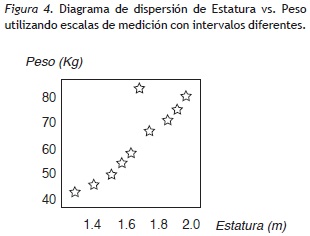
En la Figura 4 se han dejado los intervalos que realmente le corresponden a cada variable y se observa una clara correlación entre estas; existe una relación directa entre el peso de los individuos con la estatura, a excepción de un dato en esta muestra, relación imposible de considerar en la Figura 3. Con este sencillo ejemplo se muestra la importancia de utilizar la escala correspondiente de cada variable en el análisis de datos para no incurrir en este tipo de error.
La literatura científica sobre los métodos multivariados mencionados en este texto se caracteriza por la rigurosidad matemática, que aunque necesaria, puede dificultar su comprensión para el lego en estadística. Profundizar en estos métodos requiere una formación matemática elemental, gran interés y motivación de quien desee implementar alguna técnica en su investigación; para la mayoría de estos entusiastas, que no tienen una formación profunda en matemáticas, el análisis estadístico puede ser un difícil problema, situación que puede cambiar, si se aclaran los supuestos, se explican los conceptos básicos, se realizan en clase ejemplos reales, se específica el nivel de medición de las variables incluidas en el estudio y se muestra la utilidad de la técnica o prueba estadística.
Es importante mencionar que la teoría de los métodos multivariados es un campo fértil y activo, durante la última década el flujo de datos procedentes de Internet, sensores y otros dispositivos técnicos, han aumentado de forma abrupta, lo cual ha llevado a replantear las técnicas estadísticas para responder a estas exigencias (Berrendero, Justel & Svarc, 2011).
Jaques & Preda (2014), por ejemplo, han propuesto un procedimiento de agrupación para datos funcionales multivariados cuya convergencia no se ha determinado, es decir, algunas preguntas siguen abiertas y más investigaciones teóricas deben llevarse a cabo para dar respuestas.
El desconocimiento de los supuestos y finalidad de las pruebas lleva a la utilización excesiva de técnicas inadecuadas para el análisis de datos, conduciendo a errores en los resultados y a explicaciones falsas de los mismos, lo cual genera teorías con poca claridad. Más allá de lo expuesto en esta guía y de los conceptos que no pueden evitarse al presentar las distintas técnicas, se espera que la comparación de las mismas sirva para diferenciarlas, apreciar sus alcances, entender sus limitaciones, reconocer sus supuestos y profundizar en el manejo estadístico. Las técnicas se presentaron procurando incluir las más utilizadas, clasificándolas según sus objetivos de aplicación y exponiendo en cada caso sus supuestos, aunque el lector tendrá que profundizar en aspectos procedimentales que no se incluyeron en este artículo.
Particularmente, los modelos multivariados requieren de quien los utiliza un mínimo de comprensión sobre la técnica, metodología, ventajas y debilidades. Ahora bien, debido a la rigurosidad que exigen los análisis multivariados, el uso de paquetes estadísticos no es opcional. La disponibilidad de programas para el análisis estadístico como SPSS, MATLAB, R, STATISTICA, entre otros, facilitan la utilización de pruebas sofisticadas pero pueden conducir a una utilización inadecuada y mecánica de estos, de ahí la importancia de conocer la técnica, el manejo del software y la interpretación de los resultados (Field, 2013; Marques de Sá, 2007).
La utilización de procedimientos matemáticos ofrece objetividad en los resultados y esto es cierto en alguna medida, pero también acarrea una carga grande de subjetividad, donde se incluye la predilección misma del modelo matemático hasta la selección de las variables por parte del investigador.
Finalmente, los ejemplos presentados pretenden mostrar la implicación de las conclusiones a las que se llegan cuando se incumplen los supuestos mínimos que exige cada prueba. Se debe tener presente que la elección de la técnica para cada problema de investigación depende del tipo de estudio y su objetivo, de la familiaridad con los datos y lo que representan, de la confiabilidad y validez de los resultados junto con sus alcances estadísticos a la luz de una visión práctica.
Además, las pruebas estadísticas no siempre son excluyentes y en algunos casos puede resultar adecuado mezclarlas.
1 Pruebas que comparan y evalúan la probabilidad de que la distribución de la muestra de observaciones se equipare a una distribución normal.
2 Test de normalidad multivariado que evalúa la similitud de distribuciones a lo largo de varias variables.
3 Test que evalúa el supuesto de igualdad de las matrices de covarianzas de las VI en conjunto y a lo largo de los grupos.
4 Método que evalúa la existencia de diferencias significativas entre los promedio de las VI por separado.
5 El test de esfericidad de Bartlett contrasta la hipótesis nula de que la matriz de correlaciones es una matriz identidad; es decir, que existen una incorrelación lineal entre las variables.
6 Test de adecuación de la muestra para realizar un AF, valores mayores que 0.7 indican la existencia de relaciones entre las variables.
Referencias
Aparisi, F., Avendaño, G., & Sanz, J. (2006). Interpreting T2 Control Charts. IIE Transaccions, 38(8), 647-657.
Avendaño, G. (2003). Interpretación de la señal de falta de control en gráficos multivariantes mediante redes neuronales. (Doctorate Thesis), Universidad Politécnica de Valencia.
Bello, R., & Garcia, M. (1996). A model and its different applications to case-based reasoning. Knowledge System Design and Applications, 9(7), 465-473.
Berrendero, J. R., Justel, A., & Svarc, M. (2011). Principal components for multivariate functional data. Computacional Statistics and data analysis, 55(9), 2.619-2.634.
Conchillo, A. (2004). Guías doctorado. Metodología de las ciencias del comportamiento. España: Madrid: Universidad Nacional de Educación a Distancia (UNED).
Dallas, E. J. (2000). Métodos multivariados aplicados al análisis de datos. México: International Thomson Editores, S. A.
Daniel, W. (1998). Bioestadística. Base para el análisis de las ciencias de la salud. México: Noriega Editores.
Díaz, F., & Hernández, G. (2002). Estrategias docentes para un aprendizaje significativo. Una interpretación constructivista. México: McGraw-Hill.
Ferrán, M. (1996). SPSS para Windows. Programación y análisis estadístico. Madrid: McGraw-Hill.
Figueras, S. (2001). Análisis de conglomerados o clúster. Recuperado de http://www.5campus.org/leccion/cluster
Field, A. (2013). Discovering Statistics Using IBM SPSS Statistics. Fourth Edition. Londres: SAGE Publications Ltd.
Greene, J., & D'Oliveira, M. (2006). Test Estadísticos para Psicología. Madrid: McGraw-Hill.
Hair, J., Anderson, R., Tatham, R., & Black, W. (2000). Análisis Multivariante Quinta edición. Madrid: Prentice Hall.
Jackson, J. E. (1991). A user's guide to principal components. New York: John Wiley y Sons, Inc.
Jaques, J., & Preda, C. (2014). Model-based clustering for multivariate functional data. Computacional Statistics and data analysis. 71. 92-106.
Kerlinger, F., & Lee, H. (2002). Investigación del comportamiento. Métodos de investigación en ciencias sociales. México: McGraw-Hill.
Lizasoain, L., & Joaristi, L. (2003). Gestión y análisis de datos con SPSS. Versión 11. Madrid: Thompson.
López, C., Fernández, K., & Mariel, P. (2002). Índices de satisfacción del consumidor: una aplicación de modelos estructurales a la industria automovilística española. Universidad del país vasco.
Malhotra, N. (1997). Investigación de Mercados. Un enfoque práctico. México: Prentice-Hall.
Marques de Sá, J. (2007). Applied Statistics Using SPSS, STATISTICS, MATLAB and R. Second Edition. Heidelberg: Springer.
Martínez, C. (2000). Estadística y Muestreo. Bogotá: Ecoe editores.
Morales, P. (2003). El Análisis Factorial en la construcción e interpretación de tests, escalas y cuestionarios. Recuperado de http://www.upcomillas.es/personal/peter/investigacion/AnalisisFactorial.pdf
Murtonen, M. (2005). University Students' Research Orientations: Do negative attitudes exist toward quantitative methods? Scandinavian Journal of Educational Research, 49(3), 263-280.
Oquendo, D., de la Espriella, C., & Avendaño, B. L. (2007). Eventos de vida y alto afecto negativo como factores de riesgo para el desarrollo de depresión en jóvenes colombianos. (Magister), Fundación Universitaria Konrad Lorenz.
Romero, R. (1997). Curso de introducción a los métodos de análisis estadístico multivariante. Universidad Politécnica de Valencia.
Sánchez, F. (2006). Validación de una prueba para evaluar clima organizacional.
Visauta, B. (2002). Análisis Estadístico con SPSS para Windows. Segunda Edición. (Vol. 1). España: McGraw-Hill.
License
Diversitas Journal is under license Creative Commons Atribución-NoComercial-CompartirIgual 4.0 Internacional (CC BY-NC-SA 4.0)